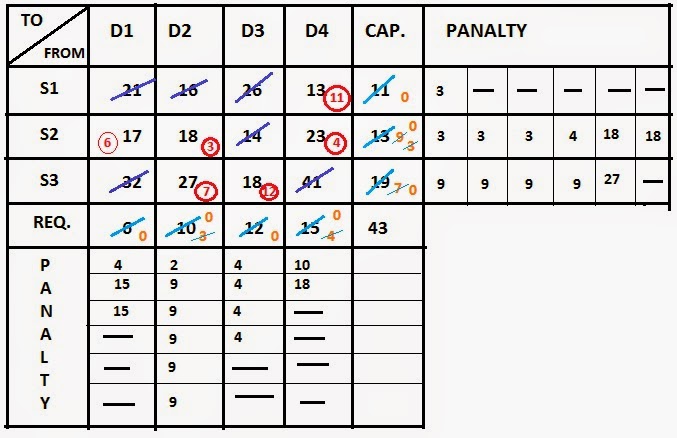
Vogel's Approximation Method with Algorithm and Example using c++
Algorithm:
Vogel's Approximation Method of Allocation.
This method also takes costs
into account in allocation. Five steps are involved in applying this heuristic:
Step 1: Determine the difference between the lowest
two cells in all rows and columns, including dummies.
Step 2: Identify the row or column with the
largest difference. Ties may be broken arbitrarily.
Step 3: Allocate as much as possible to the
lowest-cost cell in the row or column with the highest difference. If two or
more differences are equal, allocate as much as possible to the lowest-cost
cell in these rows or columns.
Step 4: Stop the process if all row and
column requirements are met. If not, go to the next step.
Step 5: Recalculate the differences
between the two lowest cells remaining in all rows and columns. Any row and
column with zero supply or demand should not be used in calculating further
differences. Then go to Step 2.
Data:
Solution:
Program:
#include<iostream.h>
#include<stdio.h>
#include<conio.h>
#include<iomanip.h>
#include<stdlib.h>
#define MAX 50
enum boolean{FALSE,TRUE};
class voggelsmethod{
int data[MAX][MAX];
int requered[MAX];
int capacity[MAX];
int allocation[MAX][MAX];
int no_of_rows,no_of_columns,no_of_allocation;
public:
lcmethod(){
for(int i=0;i<MAX;i++){
capacity[i]=0;
requered[i]=0;
for(int j=0;j<MAX;j++){
data[i][j]=0;
allocation[i][j]=0;
}
}
no_of_rows=no_of_columns=no_of_allocation=0;
}
void setColumn(int no){no_of_columns=no;};
void setRow(int no){no_of_rows=no;}
void getData();
void getCapacity();
void getRequiredValue();
void makeAllocation();
boolean checkValue(int [],int);
int getMinVal(int [],int);
int getTotalMinVal(int [],int,int);
int getMinValsPos(int,int [],int);
void display();
int getPanalty(int [],int);
};
int voggelsmethod::getPanalty(int array[],int no){
int i,j,temp;
for(i=0;i<no;i++)
for(j=i+1;j<no;j++)
if(array[i]>array[j]){
temp=array[i];
array[i]=array[j];
array[j]=temp;
}
return array[1]-array[0];
}
int voggelsmethod::getMinVal(int array[],int no){
int min=array[0];
for(int i=0;i<no;i++)
if(array[i]<min)
min=array[i];
return min;
}
int voggelsmethod::getMinValsPos(int value,int temp_data[],int no){
int k=0;
for(int i=0;i<no;i++)
if(temp_data[i]==value)
return i;
return -1;
}
int voggelsmethod::getTotalMinVal(int array[],int n,int value){
int no=0;
for(int i=0;i<n;i++)
if(array[i]==value)
no++;
return no;
}
boolean voggelsmethod::checkValue(int arr[],int no){
for(int i=0;i<no;i++)
if(arr[i]!=0)
return FALSE;
return TRUE;
}
void arrayCopy(int start,int end,int array1[],int start1,int array2[]){
for(int i=start,j=start1;i<end;i++,j++)
array2[j]=array1[i];
}
int getTotal(int array[],int no){
int sum=0;
for(int i=0;i<no;i++)
sum+=array[i];
return sum;
}
void copy2DArray(int startRow,int startCol,int endRow,int endCol,int array[][MAX],int start1Row,int start1Col,int ans[][MAX]){
for(int i=startRow,k=start1Row;i<endRow;i++,k++)
for(int j=startCol,l=start1Col;j<endCol;j++,l++)
ans[k][l]=array[i][j];
}
int getMaxVal(int array[MAX],int no){
int max=0;
for(int i=0;i<no;i++)
if(array[i]>max)
max=array[i];
return max;
}
int getMaxValPos(int array[MAX],int no,int value){
for(int i=0;i<no;i++)
if(value==array[i])
return i;
return -1;
}
void voggelsmethod::makeAllocation(){
int i=0,j=0,min,total_min;
int temp_requered[MAX]={0};
int temp_capacity[MAX]={0};
int temp_data[MAX][MAX]={0};
int position[MAX]={0};
int dataPos[MAX]={0};
int sum_of_cap,sum_of_req;
sum_of_cap=getTotal(capacity,no_of_rows);
sum_of_req=getTotal(requered,no_of_columns);
if(sum_of_cap!=sum_of_req){
if(sum_of_cap>sum_of_req){
for(j=0;j<no_of_rows;j++)
data[j][no_of_columns]=0;
requered[no_of_columns]=sum_of_cap-sum_of_req;
no_of_columns++;
}
else{
for(j=0;j<no_of_columns;j++)
data[no_of_rows][j]=0;
capacity[no_of_rows]=sum_of_req-sum_of_cap;
no_of_rows++;
}
}
i=j=0;
arrayCopy(0,no_of_rows,capacity,0,temp_capacity);
arrayCopy(0,no_of_columns,requered,0,temp_requered);
copy2DArray(0,0,no_of_rows,no_of_columns,data,0,0,temp_data);
int rowPanalty[MAX]={0};
int colPanalty[MAX]={0};
int panaltyData[MAX]={0},n=0;
while(!checkValue(temp_capacity,no_of_rows) || !checkValue(temp_requered,no_of_columns)){
for(i=0;i<no_of_rows;i++){
arrayCopy(0,no_of_columns,temp_data[i],0,panaltyData);
if(temp_capacity[i]!=0)
rowPanalty[i]=getPanalty(panaltyData,no_of_columns);
else
rowPanalty[i]=0;
}
for(i=0;i<no_of_columns;i++){
for(j=0;j<no_of_rows;j++)
panaltyData[j]=temp_data[j][i];
if(requered[i]!=0)
colPanalty[i]=getPanalty(panaltyData,no_of_rows);
else
colPanalty[i]=0;
}
int maxRowPanalty=getMaxVal(rowPanalty,no_of_rows);
int maxColPanalty=getMaxVal(colPanalty,no_of_columns);
int maxPanRow[MAX]={0};
int maxPanCol[MAX]={0};
if(maxRowPanalty>maxColPanalty){
i=getMaxValPos(rowPanalty,no_of_rows,maxRowPanalty);
for(j=0;j<no_of_columns;j++)
maxPanRow[j]=temp_data[i][j];
min=getMinVal(maxPanRow,no_of_columns);
j=getMinValsPos(min,maxPanRow,no_of_columns);
}
else{
j=getMaxValPos(colPanalty,no_of_columns,maxColPanalty);
for(i=0;i<no_of_rows;i++)
maxPanCol[i]=temp_data[i][j];
min=getMinVal(maxPanCol,no_of_rows);
i=getMinValsPos(min,maxPanCol,no_of_rows);
}
if(temp_capacity[i]>temp_requered[j]){
allocation[i][j]=temp_requered[j];
for(int k=0;k<no_of_rows;k++)
temp_data[k][j]=9999;
temp_capacity[i]-=temp_requered[j];
temp_requered[j]=0;
}
else if(temp_capacity[i]<temp_requered[j]){
allocation[i][j]=temp_capacity[i];
for(int k=0;k<no_of_columns;k++)
temp_data[i][k]=9999;
temp_requered[j]-=temp_capacity[i];
temp_capacity[i]=0;
}
else{
int k;
allocation[i][j]=temp_capacity[i];
for(k=0;k<no_of_rows;k++)
temp_data[k][j]=9999;
for(k=0;k<no_of_columns;k++)
temp_data[i][k]=9999;
temp_requered[j]=temp_capacity[i]=0;
}
n++;
}
no_of_allocation=n;
}
void voggelsmethod::getCapacity(){
cout<<"enter capacity for each source : \n";
for(int i=0;i<no_of_rows;i++){
cout<<"s"<<i+1<<" : ";
cin>>capacity[i];
}
}
void voggelsmethod::getRequiredValue(){
cout<<"enter required unit value for each destination : \n";
for(int i=0;i<no_of_columns;i++){
cout<<"d"<<i+1<<" : ";
cin>>requered[i];
}
}
void voggelsmethod::display(){
int i;
cout<<"\ngiven data :\n";
cout<<setw(9);
for(i=0;i<no_of_columns;i++)
cout<<"D"<<i+1<<setw(4);
cout<<setw(5)<<"cap"<<endl<<setw(0);
for(i=0;i<no_of_rows;i++){
cout<<setw(3)<<"S"<<i+1;
for(int j=0;j<no_of_columns;j++)
cout<<setw(5)<<data[i][j];
cout<<setw(5)<<capacity[i]<<endl;
}
cout<<setw(4)<<"req";
for(i=0;i<no_of_columns;i++)
cout<<setw(5)<<requered[i];
cout<<"\n\n after allocation :\n";
for(i=0;i<no_of_rows;i++){
for(int j=0;j<no_of_columns;j++){
if(allocation[i][j]!=0)
cout<<setw(5)<<data[i][j]<<"*"<<setw(2)<<allocation[i][j];
else
cout<<setw(8)<<data[i][j];
}
cout<<endl;
}
int k=0,sum=0;
for(i=0;i<no_of_rows;i++){
for(int j=0;j<no_of_columns;j++){
if(allocation[i][j]!=0){
cout<<"("<<data[i][j]<<" * "<<allocation[i][j]<<")";
if(k<no_of_allocation-1){
cout<<"+";
k++;
}
sum+=data[i][j]*allocation[i][j];
}
}
}
cout<<"\nanswer : "<<sum;
if((no_of_rows+no_of_columns-1)==no_of_allocation){
cout<<"\nhere "<<no_of_rows<<"+"<<no_of_columns<<"-1 ="<<no_of_allocation<<" no. of allocations";
cout<<"\n so this problem is non-degenarated solution";
}
else{
cout<<"\nhere "<<no_of_rows<<"+"<<no_of_columns<<"-1 !="<<no_of_allocation<<"no of allocations";
cout<<"\n so this problem is degenarated solution";
}
}
void voggelsmethod::getData(){
cout<<"enter source to destination data:"<<endl;
for(int i=0;i<no_of_rows;i++){
cout<<"enter "<<i<<"th row : ";
for(int j=0;j<no_of_columns;j++){
cin>>data[i][j];
}
}
}
void main(){
clrscr();
voggelsmethod v;
int r,c;
cout<<"enter no of Rows : ";
cin>>r;
cout<<"enter no of columns : ";
cin>>c;
v.setColumn(c);
v.setRow(r);
v.getData();
v.getCapacity();
v.getRequiredValue();
v.makeAllocation();
clrscr();
v.display();
getch();
}
output:
provide data:
Allocation: